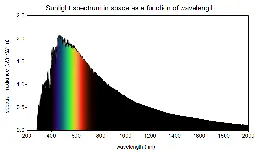
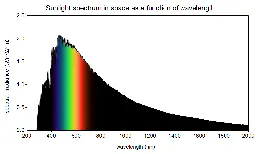
The colour of the Sun is white
The colour of the Sun is white
The color of the sun is white. The sun emits all colors of the rainbow more or less evenly and in physics, we call this combination white. That is ...
cross-posted from: https://lemmy.world/post/6080744
The sun is not yellow or orange as we see in books and movies. It emits all the colours in the visible spectrum (also in other spectrums as well) making it white!
It is white when seen from space. Here on Earth, the atmosphere disperses the blue part of the spectrum so that the blue sunlight comes to our eyes from all directions, making the sky blue. Without the blue light, the sun appears more yellow. So the color depends on your point of view :)
Wow, that's really interesting! I had no idea that the atmosphere worked as a diffuser for only a small part of the spectrum like that
It's weird that diagrams and models of our solar system still depict the sun as yellow.
Unless you're a kid in Japan, in which case it's depicted as red.
It's really a pale blue. If it were white, the visible spectrum would be pretty even, but you can see the graph is higher on the blue edge and lower on the red edge. There's enough green and red to brighten it a lot, but it's definitely blue.
In fact, the sun's surface temperature is around 5800K, and you can look up what color that actually is wherever you go light bulb shopping.
This shows the colors based on temperature, and the sun is firmly in the "Day White." It's called white, but you can see it's pretty clearly blue, especially next to the "Direct Sun" color.
It’s called white, but you can see it’s pretty clearly blue
It's more complicated than that. "White" is a completely made up term, it has no physical basis. Colors are a perception, they're not physically real. We just gave labels to some frequencies of the electromagnetic spectrum and their different combinations. And just like a camera, the human brain uses white balance correction to compensate for the fact that in different times of the day, the sunlight reaching us here on Earth has different color temperature (because it travels through different thickness of atmosphere), and by extent to compensate for different color of artificial lighting. So what our brain perceives as "white" is much dependent on context. It's how the infamous white+gold/blue+black dress illusion works. It's why when you put on ski goggles with orange lenses, the snow looks yellow at first but becomes "white" after a while. Then you take them off and the snow becomes momentarily blueish before it balances to white again. You can also force yourself to have the white balance temporarily out of sync in each eye.
If you printed out your chart and looked at it at different times of day or under different lighting conditions, what you'd think as neutral white would change too. So you can't really say which white is the "true white", it's all relative.
Colors are a perception, true, which is why we don't really talk about colors, we talk about wavelengths and temperature. 5800K is not white (relatively equal amounts of all visible light wavelengths), it's light blue (decent amounts of most visible light wavelengths, but a significant peak in the 450-500nm wavelength band, which looks blue to us). Lightbulbs use color temperature because filament and halogen lights generate light the same way the sun does: by getting hot, and how hot it is determines the light wavelengths emitted. That's why I included the chart, it's a good analogue.
If you look at the graph provided in the OP, you can see for yourself that there's significantly more blue than anything else being emitted.
It's not white, it's actually hex code FEFEFE.
I read that in the voice of Hannibal Lecter.
Am I missing something, or is the point about sunlight's spectral peak being different in frequency space than wavelength space non-sensical?
Wavelength and frequency are simply the inverse of each other, and two different ways of describing the same color. The color with peak intensity is what it is, whether you describe it unsing wavelength or frequency.
Maybe the author meant some kind of integral / area under the curve concept, since the shape of the curve is different using wavelength vs frequency as the x axis, but even then, the actual power output across some spectrum range is independent of whether you define the range in terms of wavelength or frequency.
https://www.scielo.br/j/rbef/a/mYqvM4Qc3KLmmfFRqMbCzhB/?lang=en
This is something that bothered me when I was in undergrad but now I've come to understand. The article above goes through the math of computing different Wien peaks for different representations of the spectral energy density.
In short, the Wien peaks are different because what the density function measures in a given parametrization is different. In frequency space the function measures the energy radiated in a small interval [f, f + df] while in wavelength space it measure the energy radiated in an interval [λ, λ + dλ]. The function in these spaces will be different to account for the different amounts of energy radiated in these intervals, and as such the peaks are different too.
(I typed this on a phone kinda rushed so I could clarify it if you'd like)
Hey thanks for the reply! I'll admit that paper lost me pretty quickly, so I am probably missing a subtle point. But it feels deeply unintuitive since frequency and wavelength are just two different ways of describing the same physical quantity.
So if I have a given source of photons, how the heck does the color of photons delivering most cumulative power change whether I choose to describe that color based on its wavelength or it's frequency?
Is there an analogue to something like sound energy or is this quantum physics weirdness?
(These are semi rhetorical questions... I'm not expecting you to explain unless you really feel like it 😀)